QUESTÕES COMENTADAS: PROBLEMAS DE GEOMETRIA.
1) O apótema de um quadrado inscrito em uma circunferência mede 6 cm. Calcule a medida da diagonal do quadrado.
COMENTÁRIO:
A melhor maneira de resolver questões sem figura é fazendo a figura. A figura abaixo tem os dados relevantes sobre o problema. Ela também mostra a melhor maneira de marcamos o raio da circunferência; desta forma, poderemos formar um triângulo retângulo e aplicarmos tudo que sabemos sobre esse tipo de triângulo.
 |
| QUADRADO INSCRITO EM UMA CIRCUNFERÊNCIA |
Note que a diagonal do quadrado equivale ao dobro do raio (D = 2r) e que o triângulo formado pelo raio, o apótema e o L/2 é isósceles (é fácil notar pelos ângulos) em que
L/2 = a, portanto o lado vale 12 cm.
Agora, aplicamos o teorema de Pitágoras no quadrado:
D² = L² + L² => D² = 12² +12²
portanto, a diagonal do quadrado é
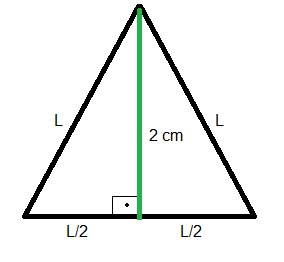
2) A altura de um triângulo equilátero mede 2 cm. Determine seu perímetro e sua área.
COMENTÁRIO:
Para calcularmos
o perímetro e a área, devemos obter o lado do triângulo. Para isso, traçando a
altura do triângulo equilátero, dividimos um de seus lados em duas partes
iguais e formamos um ângulo reto na base, como mostra a figura (Note que isso
não acontece com qualquer triângulo). Podemos aplicar o teorema de Pitágoras ou
até mesmos as razões seno e tangente para o ângulo de 60º. Por Pitágoras,
temos:
Calculando o perímetro:
O perímetro P é a
soma de todos os lados de um polígono, logo:
Calculando a área:
Existe uma
fórmula para calcular a área de um triângulo equilátero (e apenas o equilátero)
sem a altura, mas a questão nos fornece a altura, por isso não lançaremos mão
desse recurso.
A área de um triângulo qualquer é dada por
No problema, a base é o lado e a altura vale 2 cm. Portanto,
3) A diagonal de um quadrado mede 3√6 cm. Determine seu perímetro e sua área.
COMENTÁRIO:
Tanto para o cálculo do perímetro como o cálculo da área, necessitamos do lado do quadrado.
Vamos explorar agora as razões trigonométricas.
A diagonal de um quadrado é também bissetriz dos ângulos por onde ela passa (lembre-se que bissetriz é um segmento que divide um ângulo em duas partes iguais), portanto o ângulo formado pela diagonal e o lado é de 45º. Observe a figura:
Tanto para o cálculo do perímetro como o cálculo da área, necessitamos do lado do quadrado.
Vamos explorar agora as razões trigonométricas.
A diagonal de um quadrado é também bissetriz dos ângulos por onde ela passa (lembre-se que bissetriz é um segmento que divide um ângulo em duas partes iguais), portanto o ângulo formado pela diagonal e o lado é de 45º. Observe a figura:
portanto,
Como já encontramos o lado, basta
multiplicar por 4 para obtermos o perímetro e como a área de um quadrado é lado
vezes lado (lado ao quadrado), basta aplicarmos a fórmula.
O perímetro é
A área é
4) O perímetro de um quadrado inscrito em uma circunferência é 40 cm. Determine a medida do raio.
COMENTÁRIO:
COMENTÁRIO:
Observe a figura.
Lembre-se que o apótema divide o lado do polígono regular em duas partes iguais.
Aplicando o cosseno para o ângulo de 45º, temos:
5) Do alto de uma torre de 50 metros de altura, localizada em uma ilha, avista-se a praia sob um ângulo de 45º em relação à horizontal. Qual é a distância da torre à praia?
COMENTÁRIO:
Essa questão é a mais fácil de todas. Basta você conseguir identificar que o triângulo formado é isósceles, pois a torre e a distância dela à praia é a mesma.
Argumentos:
1. A torre forma um ângulo reto com a horizontal.
2. Um dos outros ângulo é 45º.
3. Como a soma dos ângulos internos de um triângulo é 180º, o outro ângulo só poderá ser de 45º.
4. Se um triângulo tem dois ângulos iguais, então ele tem (pelo menos) dois lados iguais.
Observe a figura.
Resposta: 50 metros
6) Determine o valor de
x sabendo que b = √75 cm e c = 15 cm.
COMENTÁRIO:
Para resolver essa
questão, é necessário usar a razão tangente:
O único ângulo que possui esse valor de tangente é o ângulo de 30º.
7) Calcule o perímetro
de um triângulo equilátero inscrito em uma circunferência cujo raio mede 7√3 cm.
COMENTÁRIO:
8)Prove que
COMENTÁRIO:
A figura abaixo representa um triângulo equilátero inscrito em uma
circunferência com o raio indicado na questão.
Aplicando o cosseno para o ângulo (de 30º) formado pelo raio (em vermelho) e L/2, temos:
Para calcular o perímetro, basta multiplicar o lado por 3, pois o triângulo é equilátero.
COMENTÁRIO:
Para provar isso, vamos considerar um
triângulo retângulo em que um dos ângulos seja a (indicado na figura), como o da figura.
Então, substituindo:
Mas, pelo teorema de Pitágoras,


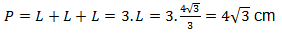















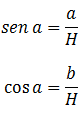




Comentários
Postar um comentário